作者：bluebird118

上篇文章简单介绍了LOOKUP函数的基本应用，如果要全面了解Lookup函数，必须要懂LOOKUP函数的二分法，也就是lookup的查找原理。在这里，我们以上文中的例子来说明，来直接上图:  

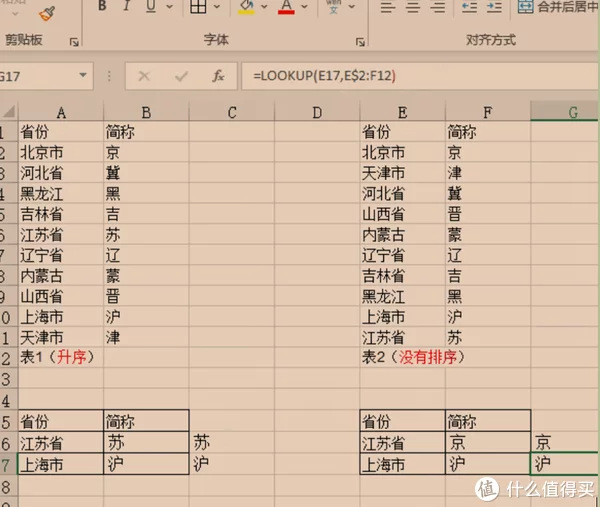
这里以江苏省为例上面的公式分别是

=Lookup(A16,A2:B11)；=Lookup(E16,E2:F11)；

上面相同的公式，具有不同的结果。因此，你看了下面的关于二分法的说明，就能明白其中的缘由。

一、什么是二分法。

一个一个依次进行查找，这就是是遍历法。二分法与之不同。二分法，如其名，二分，或者说是每次对半砍。也就是从二分位处进行查找，若找不到，再从下一个二分位处查找，直到查找到和他大小相同或比它小的数。

二、基本原理。

1、二分位的判定

当总数字是奇数时，二分位很好判定，中间的数字即可。如有9个数（也就是该函数的第二个参数），则第5个数就是中间的数。

如果有10个数呢，则第5个位置是二分位。有一个公式可以计算：=INT((总行数+1)/2)

2、查找方向确定

当在二分位查找不到时，接下来该怎么操作呢？

如果上一次二分位值大于查找的值时，则向上接着查找，找出新的二分位，直到找出对应的值。如下图。

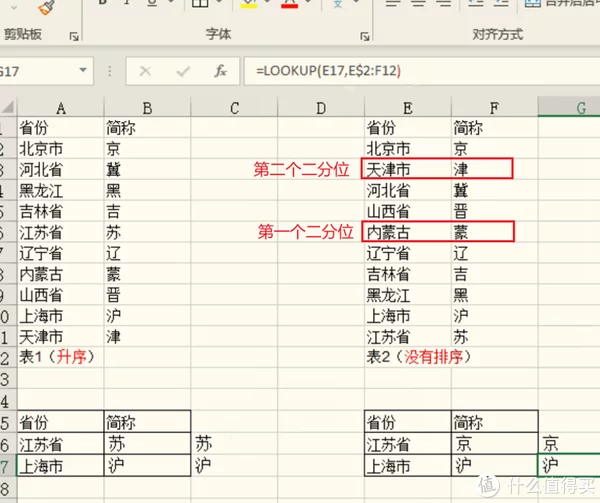
在上图，左边的数据是按照升序来排列的，我们来看右边的数据，查找的值（江苏省的值）是小于二分位值（内蒙古的值），没有找到“江苏省”，公式则会向上找第2个二分位，第2个二分位是天津市（江苏省的值仍然是小于天津市的值），公式仍然会往上找，因上面只有一个值是北京市，所以公式最终返回的值是“京”。

同理，如果数值小于查找的值时，向下继续查找。在这里以查找值（上海市）为例，第1个二分位的值（内蒙古的值是小于上海市的值），方向向下；第2个二分位的值（黑龙江的值仍然是小于上海市的值），方向向下。

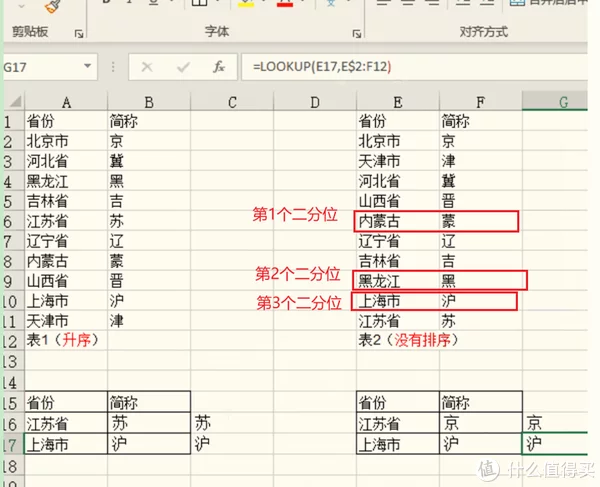
如果存在多种重复的值，其中二分值等于查找的值，向下逐个查，直到相邻且相等的值即符合条件。

截止到这里，大家应该能够明白lookup的查找原理，也明白为什么直接利用函数公式，则需要进行排序，排序后，公式返回的结果才是正确的。

今天我们就来了解通过LOOKUP查询返回最后一个满足条件的情况的应用实例。先上菜：

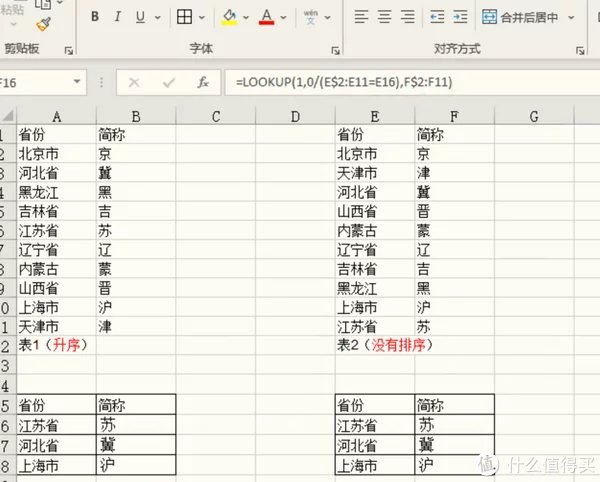
具体公式为=lookup（1，0/(e2:e11=e16),f2:f11）

下面我们来看下具体的原理，原理清楚了，这个公式就好记了，基本上就是一个套路或者说是模板，如果你只想解决问题，那么直接套用即可，可以告诉你100%返回最后一个满足条件对应的结果。

来上大餐（以上文的例子有点不恰当，不过也能说明其中的原理。在这里，就不费脑筋来寻找新的例子）：

遇到这种需求，在这里肯定不能直接用Lookup查找江苏省，否则按二分位查找，结果不一定是最后一个。所以就用0除的方法把符合条件的变成0，不符合条变成错误值：

=0/(e2:e11=e16)

结果如下{#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;#DIV/0!;0}

由于lookup会过滤掉错误值，所以在lookup眼中，上面的数组是这样的：

{0}

然后用1查找最后一个0的位置

=lookup（1，0/(e2:e11=e16),f2:f11）

这里1是任一个大于0的值，因为大于0，所以用二分法查找时，会一直向下查找，直到最后一个0值。

引申一下：

如果数据中存在多个重复数据，可以用上述公式得出最后一个值。同样可以用lookup函数来满足多条件的查找。比如：LOOKUP(1,0/((A2:A9=E2)*(B2:B9=F2)),C2:C9)。在这里需要注意的是Lookup() 多条件查找时无需排序，正常LOOKUP函数要求“查找区域”中的值必须按升序排列，因为是二分法原理，即lookup的二分法查找，是跳跃式的查找。它总认为被查找的1组值是从小到大排列，如果遇到小的就向下找更大的，如果遇到大的就向上找更小的。